For Which Intervals Below Is The Average Rate Of Change Less Than Or Equal To Zero?

Measurement levels refer to different types of variables
that imply how to clarify them. Standard textbooks distinguish 4 such measurement levels or variable types. From low to loftier, these are

nominal variables;
ordinal variables;
interval variables;
ratio variables.

The "higher" the measurement level, the more information a variable holds. The unproblematic flowchart below shows how to classify a variable.

Measurement Levels - Classical Approach

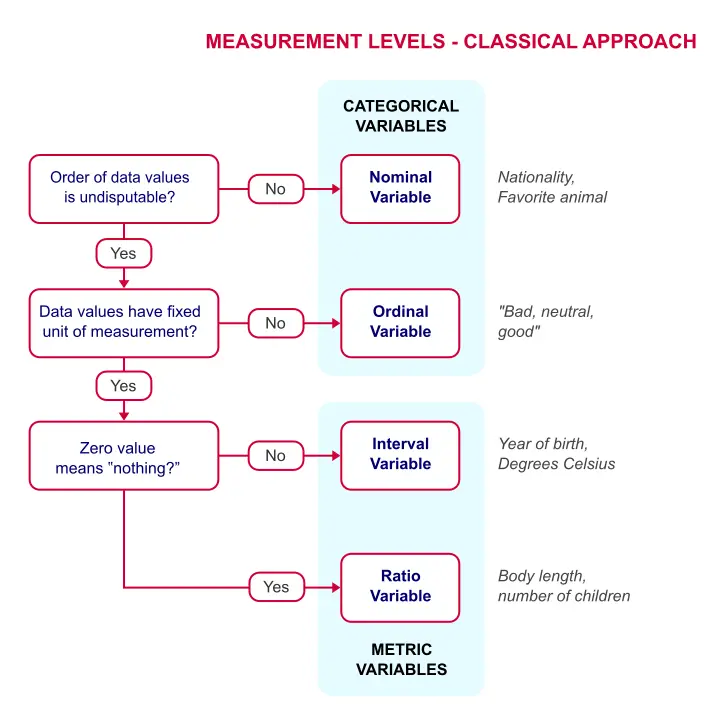Quick Overview of Measurement Levels

Let's at present take a closer look at what these variable types really hateful with some examples.

Nominal Variables

A nominal variable is a variable whose
values don't have an undisputable order. So let'southward say we asked respondents in which country they live and the answers are

holland;
Belgium;
France;
Germany;
Luxembourg.

So what'due south the correct order for these countries? Well, we could sort them alphabetically, co-ordinate to their sizes or to numbers of inhabitants. Different orders make sense for a list of countries. In short, countries don't have an undisputable order and therefore "country" is a nominal variable.
Now, countries may exist represented by numbers (one = Netherlands, 2 = Belgium and and so on) in SPSS or some other data format. These numbers exercise have an undisputable order. But state is still a nominal variable considering what'south represented by these numbers -countries- does not have an undisputable order.

Frequency Distribution Example Nominal Variable

Country -fifty-fifty if represented as numbers- is still a nominal variable

In a similar vein, ZIP codes -representing geographical areas which don't have a clear order- are nominal as well. But prices in dollars -representing amounts of money- obviously do have an undisputable gild and hence are not nominal.

Ordinal Variables

Ordinal variables hold values that have an undisputable order
merely no fixed unit of measurement. Some fixed units of measurement are meters, people, dollars or seconds. Nevertheless, there's no fixed unit of measurement for a question like "how did you similar your nutrient?" with the post-obit answer categories:

Bad;
Neutral;
Skillful.

Some may argue that Bad = one betoken, Neutral = 2 points and Expert = 3 points. Only that'south but a wild guess. Perhaps our respondents experience Neutral represents ane.5 or 2.5 points. This is illustrated past the effigy below.

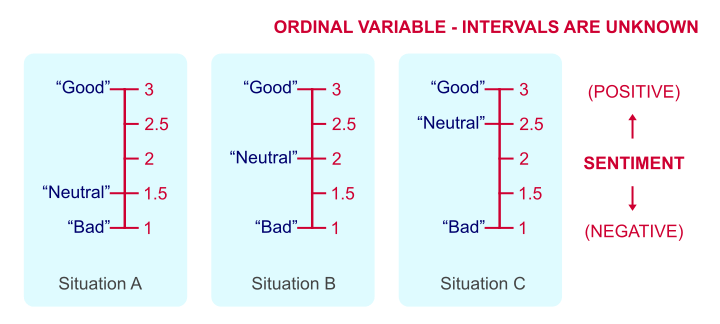Intervals between reply categories are unknown for ordinal variables.

Nosotros've no way to prove which scenario is true because just "points" are not a stock-still unit of measurement of measurement. And since we don't know if Neutral represents 1.five, 2 or 2.5 points, calculations on ordinal variables are non meaningful. Less strictly though, calculations on ordinal variables are quite common under the Assumption of Equal Intervals.

Besides annotation that monthly income measured as

Less than € 1000,-;
€ thou,- to € 2000,-;
€ 2000,- or over.

is ordinal. Euros are a fixed unit just the answers are income categories, not numbers of Euros.

Interval Variables

Interval variables have a stock-still unit of measurement
but zippo does not mean "nix". One of the rare examples is "in which year did it happen?" Ignoring leap days, years are a fixed unit of measurement of measurement for time. Nevertheless, the year zero doesn't mean "nothing" with regard to fourth dimension.
As a outcome, multiplication is not meaningful for interval variables. The yr 2000 isn't "twice as late" as the year 1000. The same goes for temperature in degrees Celsius: zero degrees is not "nix" with regard to temperature. Therefore, 100 degrees is not twice as hot as 50 degrees. This argument could, however, exist made for temperature in Kelvin.
Nosotros should add together that these are the but 2 examples of interval variables we could call up of. Interval variables are e'er analyzed similarly to ratio variables -which we'll turn to adjacent. But distinguishing these as separate measurement levels -all textbooks still practise- is pointless.

Ratio Variables

Ratio variables accept a fixed unit of measurement
and zilch actually means "zippo." An example is weight in kilos. A kilo is a stock-still unit of measurement because information technology always represents the exact same weight. Too, zero kilos corresponds to "goose egg" with regard to weight. As a effect, multiplication is meaningful for ratio variables. In fact, nosotros don't need more than than a kitchen scale to bear witness that 2 times 1 kilo really is the same corporeality of weight as 1 fourth dimension two kilos.

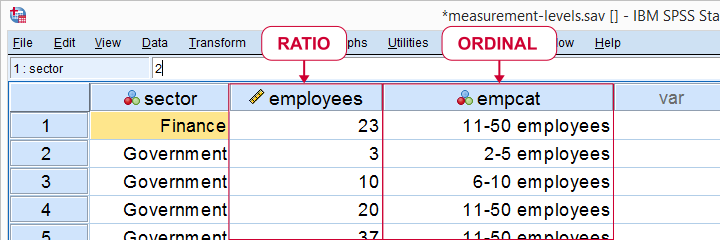Data with Variable Measured at Both Ratio and Ordinal Level

Number of employees as ratio as well equally ordinal variable

Some text books mention an "accented zero point". We rather avoid this phrasing considering ratio variables may agree negative values; the balance of my bank account may exist negative but is has a fixed unit of measurement -Euros in my example- and zero ways "aught".

Classical Measurement Levels - Shortcomings

We argued that measurement levels affair because they facilitate data analysis. However, when nosotros look at common statistical techniques, we run across that

dichotomous variables are treated differently from all other variables but classical measurement levels fail to distinguish them;
metric variables (interval and ratio) are e'er treated identically;
categorical variables (nominal and ordinal) are sometimes treated similarly and sometimes not.

Considering of these reasons, nosotros recollect the nomenclature below is much more helpful.

Measurement Levels - Modern Approach

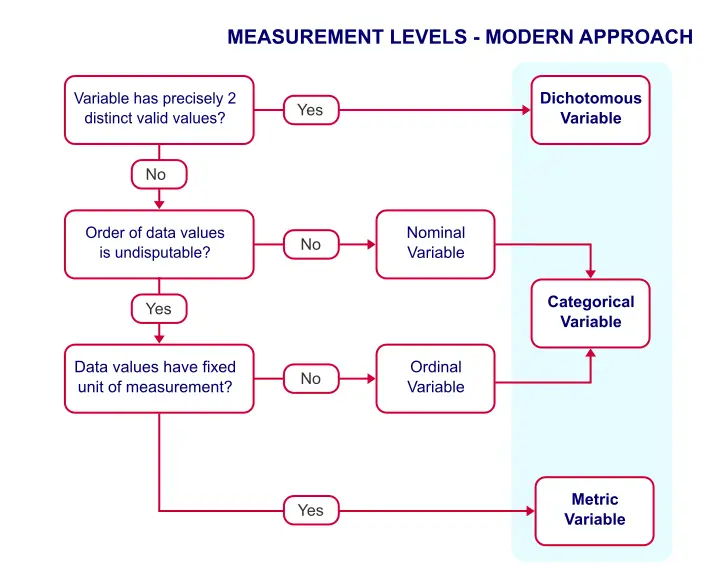
This nomenclature distinguishes 3 main categories which we'll briefly discuss.

Dichotomous Variables

Dichotomous variables have precisely two distinct values. Typical examples are sex, owning a car or carrying HIV. Information technology is useful to distinguish dichotomous variables equally a separate measurement level considering they crave different analyses than other variables:

an contained samples t-test tests if a dichotomous variable is associated with a metric variable;
a z-test and Phi-coefficient are used to examination if 2 dichotomous variables are associated;
logistic regression predicts a dichotomous issue variable.

Categorical Variables

Categorical variables are variables on which
calculations are not meaningful. Therefore, nominal and ordinal variables are categorical variables. They contain (usually few) answer categories. Because calculations are non meaningful, categorical variables merely define groups. We therefore analyze them with frequency distributions and bar charts.

Metric Variables

Metric variables are variables on which
calculations are meaningful. That is: interval and ratio variables are metric variables. Because calculations are allowed, nosotros typically clarify them with descriptive statistics such as

means;
standard deviations;
skewnesses.

Data Analysis - Next Steps

We merely argued that

chiselled variables define groups of cases and
we use descriptive statistics for analyzing metric variables.

Now, say we'd similar to know if two categorical variables are associated. Then the showtime variable defines groups and the second variable defines groups within those groups. A table that shows just that is a contingency tabular array as shown below. It basically holds frequency distributions within frequency distributions

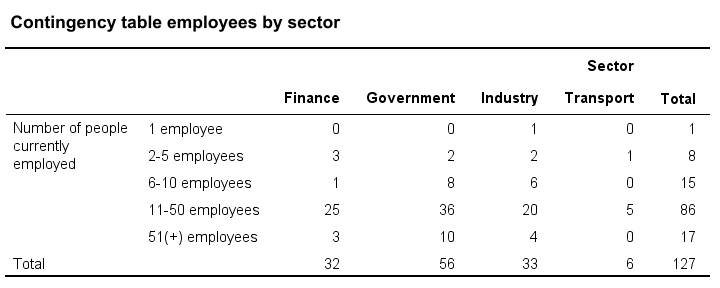
Contingency Table for 2 Categorical Variables

Next, we could visualize the association with a stacked bar chart. Or nosotros may examination if the association is statistically significant past running a chi-square independence exam on our contingency table.

Or perchance nosotros'd like to know if a categorical variable and a metric variable are associated. The categorical variable defines groups. Within those groups, we'll audit descriptive statistics over our metric variable. We thus arrive at the tabular array as shown below.

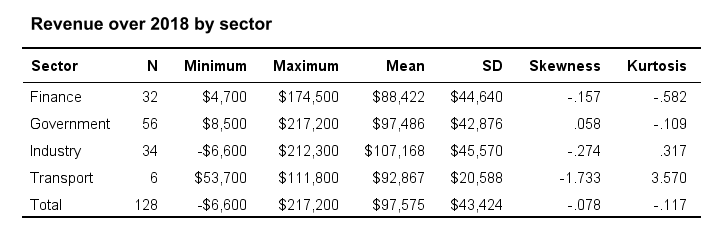
Table with Descriptive Statistics over Metric Variable by Categorical Variable

We could visualize the means as a bar nautical chart for means past category. Or we could test if the population means differ past category with ANOVA.

And so now nosotros run into how measurement levels assist the states choose the right analyses. For a more complete overview of analyses by measurement level, encounter SPSS Information Analysis - Bones Roadmap.

Cheers for reading!